 Эвальд Ильенков в юности. Фото из архива Елены Иллеш, дочери Э.В.Ильенкова.
Эвальд Ильенков в юности. Фото из архива Елены Иллеш, дочери Э.В.Ильенкова.В этом году конференция пройдет в формате экспертных коллоквиумов. Ведущие эксперты в сфере образования и психологии будут говорить о роли мышления, инструментах и технологиях его развития, о принципах построения содержания образования и образовательной среды для развития мышления.
В ходе конференции состоятся экспертные коллоквиумы по темам:
Школа и мышление: постановка вопроса на уровне образовательной политики (куратор: Реморенко И.М.)
Таксономия и оценка мышления в образовании (куратор: Фрумин И.Д.)
L.S.Vygotsky vs J.Piaget: два подхода к исследованию развития мышления в психологии и образовании (кураторы: Щедровицкий П.Г., Рубцов В.В.)
Мышление и развивающее обучение (куратор: Львовский В.А.)
Среди ключевых спикеров конференции: Аркадий Марголис, Виталий Рубцов, Петр Щедровицкий, Исак Фрумин, Игорь Реомренко, Борис Эльконин, Александр Асмолов, Владимир Львовский.
Конференция ориентирована не только на исследователей и разработчиков в области содержания и методов обучения, но и на руководителей школ, учителей и методистов.
Подробная информация о конференцииРегистрация для участияВиталий Рубцов о конференции
Участие в Конференции — очное. Рабочий язык – русский.
Дата проведения конференции:
18 октября – ул. Садовая-Самотечная, д.8, МГПУ;
19 октября – ул. Сретенка, д.29, МГППУ.
www.mgppu.ruПроезд: ст. м.«Сухаревская»: выход из метро налево. Далее через арку мимо «Макдональдса». 1 минута от метро.
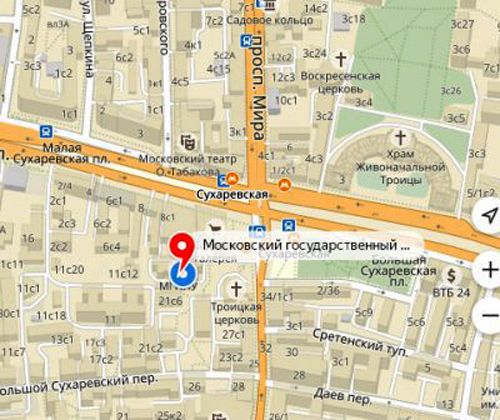 Схема проезда
Схема проезда Эвальд Ильенков с дочерью Еленой Иллеш. Фото из архива Елены Иллеш.
Эвальд Ильенков с дочерью Еленой Иллеш. Фото из архива Елены Иллеш....Уже ближайшие шаги в сфере математического мышления, которые он неуверенно делает под присмотром учителя, заводят его в тупик и сбивают с толку. Скоро оказывается, что единичный предмет, который ему показывают, вовсе не обязательно называется словечком «один», что это может быть и «два» (две половинки), и три, и восемь, и вообще сколько угодно. Оказывается, что число «1» есть все что угодно, но только не название единичной, чувственно-воспринимаемой «вещи». А чего же? Какую реальность обозначают числовые знаки?
Теперь этого вам уже не скажет и ребенок, обладающий самыми тонкими и гениальными аналитическими способностями... И не скажет потому, что в его голове отложились два взаимоисключающих представления о числе, которые он никак не соотносит, не «опосредует». Они просто находятся «рядом», как два стереотипа, в его «второй сигнальной системе».
Это очень легко выявить, столкнув их в «сшибке», в открытом противоречии.
Покажите ему игрушечный поезд, сцепленный из трех вагонов и паровозика. Сколько?
Один (поезд)? Четыре (составных части поезда)? Три и один (паровоз и вагоны)? Шестнадцать (колес)? Шестьсот пятьдесят четыре (грамма)? Три пятьдесят (цена игрушки в магазине)? Одна вторая (комплекта)?
Здесь обнаруживается все коварство абстрактного вопроса «сколько?» на который его ранее приучили давать бездумно абстрактный ответ, не уточняя – «чего?»... И даже отучая от такого желания уточнить, если оно у него было, как от желания, которое надо оставить перед входом в храм математического мышления, где в отличие от мира его непосредственного опыта и вкусная конфета, и отвратительная ложка касторки значат «одно и то же» – а именно «одно», единицу»...
Такая абстракция, на которую ребенка «натаскивают» первые страницы обучения «счету», приучающие начисто отвлекаться от всякой качественной определенности «единичных вещей», приучающие к мысли, что на уроках математики «качество» вообще нужно забыть во имя чистого количества, во имя числа, для понимания ребенка непосильна. Он ее может только принять на веру – так, мол, уж принято в математике, в противоположность реальной жизни, где конфету от касторки он все же продолжает различать...
Предположим, что ребенок твердо «усвоил» вышеразъясненное представление о «числе» и «счете», и что три арбуза – «одно и то же», что и три пары ботинок, – «три» без дальнейших разъяснений.
Но тут ему сообщают новую тайну – три аршина нельзя складывать с тремя пудами, это – «не одно и то же», и что, прежде чем «складывать» – располагать в один счетный ряд – надо предварительно убедиться, что имеешь дело с одноименными (однокачественными) вещами, что бездумно складывать и вычитать можно только «неименованные числа», а именованные – нельзя... Еще один стереотип, причем – прямо противоположный. Какой же из них следует «применить», «включить» в данном случае?
Почему в одном случае надо и можно «складывать» два мальчика с двумя вишенками, а в другом – не надо и нельзя? Почему в одном случае это – «одно и то же», а именно – единичные чувственно-воспринимаемые вещи без дальнейших разъяснений, а в другом – «не одно и то же», – разноименные, разнородные (хотя и тоже единичные) вещи?
В самом деле – почему?
Учитель этого не объясняет. Он просто показывает – на «наглядных примерах» что в одном случае надо действовать так, а в другом – эдак. Тем самым ребенку внушаются два готовых абстрактнейших представления о «числе» и не дается его конкретного понятия, то есть понимания...
Это очень напоминает дидактические принципы обучения «уму», высмеянные мудрой народной сказкой.
– Дурень, а дурень, чем на печке лежать – пошел бы, потерся около людей – ума набрался!
Послушный и прилежный дурень увидел мужиков, что таскали мешки с пшеницей, и ну – тереться то об одного, то об другого...
– Дурень ты, дурень, тут надо было сказать – таскать вам, не перетаскать!
Дурень послушно следует и этому ценному указанию...
Учителя и здесь полагали, что «конкретно» – с помощью нагляднейшего словечка – «потереться» – объяснили ему, как можно «набраться ума».
Но ведь ребенок, как и дурень в сказке, не понимает мудреных иносказаний взрослых. Он их понимает буквально, охватывая в их словах и объяснениях только то, что ему близко и понятно из его собственного жизненного опыта. И поскольку его опыт гораздо беднее, чем опыт взрослых и выражающие этот опыт слова, то он в этих словах улавливает лишь часть заключенного в них смысла, понимая их буквально абстрактно. То есть односторонне, очень общо. В результате вместо конкретного понимания (и под видом такового) он усваивает и принимает к сведению и к руководству крайне абстрактно-общий (а потому и коварно-двусмысленный) рецепт... То же и с «числом».
На развитие сайта
